A. LÝ THUYẾT – ÔN THI TOÁN LỚP 6 HỌC KỲ 1
I. SỐ HỌC (ÔN THI TOÁN LỚP 6 HỌC KỲ 1)
Chương I → Ôn tập và bửa túc về số từ nhiên1) Tập hợp, bộ phận của một tập phù hợp – Tập hợp của các số từ bỏ nhiên, ghi số từ nhiên
Tập hợp là một loại có mang cơ bạn dạng thường được dùng ở vào toán học và ở trong đời sống, ta vẫn hiểu được tập hợp thông qua những ví dụ bên dưới.
Bạn đang xem: Ôn tập toán lớp 6 học kì 1
Để viết được một tập hợp, ta sẽ sở hữu thể:
– Liệt kê những bộ phận của một tập hợp.
– chỉ ra được những tính chất đặc trưng dành cho các bộ phận ở vào tập hợp.
Để biểu lộ ký hiệu a là một phần tử phía trong tập hợp A, ta sẽ viết a ∈ A. Để biểu lộ ký hiệu b không là thành phần nằm vào tập thích hợp A, ta viết b ∉ A.
Tập hợp của những số tự nhiên thì được kí hiệu là N.
N = 0;1;2;…
Tập hợp của các số tự nhiên và thoải mái khác 0 thì được kí hiệu là N*.
N* = 1;2;3;…
Mỗi số tự nhiên và thoải mái thì được biểu diễn bởi một điểm nằm trong tia số. Ở bên trên tia số, điểm để màn biểu diễn số nhỏ nằm ở phía bên trái của điểm màn biểu diễn số lớn.
Trong một hệ thập phân, cứ bao gồm mười đơn vị ở một mặt hàng thì sẽ làm cho thành một đơn vị chức năng ở mặt hàng trên ngay tắp lự trước đó.
Để ghi được số thoải mái và tự nhiên ở vào hệ thập phân, bạn ta phải sử dụng mười chữ số là: 0,1,2,3,4,5,6,7,8,9. Ở trong hệ thập phân, cực hiếm của từng số phía trong một hàng sẽ thay đổi dựa theo địa chỉ của số đó.
2) Số phần tử của một tập thích hợp – Tập phù hợp con
Những kỹ năng cần nhớ:
Một tập phù hợp thì có thể chứa 1 phần tử, đựng được nhiều phần tử, cất vô số phần tử, cũng có thể là không chứa một trong những phần tử nào.
Tập hợp cơ mà không có phần tử nào thì được gọi là 1 tập phù hợp rỗng. Tập đúng theo rỗng tất cả kí hiệu là ø.
Nếu như mọi phần tử của một tập vừa lòng A đều phía trong (thuộc) tập phù hợp B thì tập vừa lòng A là được call là tập hợp nhỏ của tập vừa lòng B. Kí hiệu là: A ⊂ B, ta đọc là : tập hợp A là tập hợp nhỏ của tập hòa hợp B, hay là tập vừa lòng A được chứa trong tập đúng theo B, hoặc là tập phù hợp B cất tập đúng theo A.
Nếu A ⊂ B và B ⊂ A thì ta vẫn nói rằng: A cùng B là nhị tập hợp bằng nhau, kí hiệu là: A = B.
3) Phép cộng và phép nhân
Tính chất giao hoán nghỉ ngơi trong phép nhân và phép cộng:
Khi đổi chỗ phần nhiều số hạng của một tổng thì tổng đó sẽ không thay đổi.
Khi thay đổi chỗ phần lớn thừa số của một tích thì tích đó sẽ không thay đổi.
Tính chất phối hợp giữa phép nhân cùng phép cộng:
Muốn chiếu lệ tính cộng một tổng của nhị số với một số trong những thứ ba khác, ta rất có thể làm phép tính cộng số thứ nhất với số thứ hai cùng với số máy ba.
Muốn chiếu lệ tính nhân một tích của nhị số với một trong những thứ bố khác, ta hoàn toàn có thể làm phép tính nhân số đầu tiên với tích thân số trang bị hai với số thứ ba.
Tính chất trưng bày giữa phép nhân so với phép cộng:
Muốn chiếu lệ tính nhân một trong những với một tổng, ta có thể làm phép tính nhân số đó với từng số hạng của tổng rồi cộng các tác dụng đã ra lại với nhau.
4) Phép trừ với phép chia
Điều khiếu nại để rất có thể thực hiện được một phép tính trừ là số bị trừ phải lớn hơn hoặc bằng số trừ.
Điều kiện để a hoàn toàn có thể chia hết mang lại b (a,b ∈ N, b ≠ 0) là có: số tự nhiên q sao cho a = b.q
Trong một phép chia tất cả dư :
Số bị chia = số phân chia x yêu mến + số dư
Số phân chia lúc nào thì cũng khác 0. Số dư thời điểm nào cũng nhỏ hơn số chia.
5) Lũy thừa với số mũ tự nhiên và thoải mái – Nhân hai lũy thừa cùng cơ số – phân tách hai lũy thừa thuộc cơ số
Các kỹ năng và kiến thức cần nhớ
Lũy vượt bậc n của một số trong những a là tích của n quá số của a:
a^n = a.a………a (n ∈ N*, n là vượt số)
Khi nhân nhị lũy thừa có cùng cơ số, ta sẽ giữ nguyên cơ số đó cùng cộng các số mũ lại với nhau, ta được:
a^m . A^n = a^(m+n)
Khi chia hai lũy thừa gồm cùng cơ số, ta sẽ giữ nguyên cơ số đó cùng trừ những số mũ với nhau, ta được:
a^m : a^n = a^(m+n)
Quy ước: a^0 = 1 (a ≠ 0)
6) tín hiệu chia hết mang đến 2, phân chia hết đến 5; tín hiệu chia hết cho 3, chia hết mang lại 9
Những số gồm chữ số ngơi nghỉ tận thuộc là phần đông chữ số chẵn thì chia được hết cho 2 cùng chỉ bao hàm số đó mới rất có thể chia được hết mang đến 2.
Những số bao gồm chữ số sống tận cùng là số 0 hoặc số 5 thì phân tách được hết đến 5 và chỉ bao gồm số đó mới có thể chia được hết mang đến 5.
Những số mà gồm tổng rất nhiều chữ số chia được hết được đến 9 thì rất có thể chia được hết cho 9 với chỉ bao hàm số đó new chia được hết đến 9.
Những số mà tất cả tổng của những chữ số chia được hết mang lại 3 thì phân tách được hết mang lại 3 và chỉ các số kia mới có thể chia được hết cho 3.
7) Ước cùng bội – hợp số – Số nhân tố – Phân tích một số trong những ra thừa số nguyên tố
Nếu như một số trong những tự nhiên a phân tách được không còn cho một trong những tự nhiên b thì a được call là bội số của b, còn b thì được điện thoại tư vấn là mong số của a.
– hy vọng tìm ra được bội số của một vài khác 0, ta sẽ làm phép tính nhân số đó lần lượt với chữ số 0,1,2,3… Bội của một số trong những b sẽ có được dạng tổng quát là: b.k cùng với k ∈ N.
– ao ước tìm ra được ước số của một trong những khác 0, ta đã lần lượt chiếu lệ tính chia số đó cho các chữ số 1,2,3… để xét xem như là số đó gồm chia không còn cho phần nhiều số nào.
Số nguyên tố là số tự nhiên có giá bán trị lớn hơn 1, không tồn tại ước số khác 1 với khác chủ yếu nó. Phù hợp số là số thoải mái và tự nhiên có giá chỉ trị lớn hơn 1, có ước số khác 1 với khác chủ yếu nó. Số nguyên tố có giá trị nhỏ dại hơn 2, đó đó là số nguyên tố chẵn duy nhất.
Để phân tích một số trong những tự nhiên ra được vượt số nhân tố là ta vẫn viết số đó ở dưới dạng đông đảo thừa số nguyên tố. Từng số tự nhiên có giá bán trị to hơn 1 đều có thể phân tích được ra thành quá số nguyên tố.
8) Ước chung và bội chung – Bội chung nhỏ dại nhất – Ước chung khủng nhất
Ước tầm thường của hai hoặc nhiều số là mong số của toàn bộ những số đó.
Bội phổ biến của nhì hoặc các số là bội số của tất cả những số đó.
Ước chung lớn số 1 (ƯCLN) của hai hoặc các số lớn số 1 trong và một tập hợp cầu chung của những số đó.
* Muốn tìm kiếm được ƯCLN của nhì hoặc nhiều số, ta sẽ triển khai ba cách như sau:
Bước 1: so sánh được mỗi số ra làm cho thừa số nguyên tố.
Bước 2: chọn ra được phần lớn thừa số yếu tố chung.
Bước 3: sinh sản lập phép tính tích của những thừa số đó, mỗi thừa số sẽ được lấy cùng với số mũ nhỏ nhất của nó. Tích đó chính là ƯCLN phải tìm.
Hai hoặc các số mà có ƯCLN là một trong những thì hotline là mọi số nguyên tố cùng nhau
Trong phần nhiều số vẫn cho, ví như như số nhỏ dại nhất là mong số của không ít số còn sót lại thì ƯCLN của rất nhiều số sẽ cho chính là số nhỏ tuổi nhất đó.
Để tìm kiếm được ước chung của không ít số đang cho, ta hoàn toàn có thể tìm ra những ước số của ƯCLN của những số đó.
Bội chung nhỏ dại nhất (BCNN) của hai hoặc nhiều số chính là số nhỏ nhất không giống 0 sinh hoạt trong tập hòa hợp bội chung của những số đó.
* Muốn tìm được BCNN của hai hoặc các số ta sẽ tiến hành ba cách như sau:
Bước 1: so sánh được mỗi số ra làm thừa số nguyên tố.
Bước 2: lựa chọn ra được đông đảo thừa số nguyên tố thông thường và phần đa thừa số nguyên tố riêng.
Bước 3: sinh sản lập phép tính tích của những thừa số đó, mỗi thừa số sẽ được lấy cùng với số mũ lớn số 1 của nó. Tích đó chính là BCNN phải tìm.
Nếu như những số đã đến từng đôi một bao gồm nguyên tố cùng mọi người trong nhà thì BCNN của chúng sẽ là tích của những số đó.
Trong hồ hết số sẽ cho, nếu như số lớn số 1 là bội của những số còn sót lại thì BCNN của không ít số đang cho đó là số lớn số 1 ấy
Để tìm thấy được bội chung của các số đã cho, ta rất có thể tìm được phần nhiều bội số của BCNN của những số đó.
Chương II → Số nguyên1) Tập hợp đa số số nguyên bao hàm những số nguyên âm, số 0 và đầy đủ số nguyên dương
Z = …-3;-2;-1;0;1;2;3;…
2) Số đối của một số nguyên a đó là –a lấy một ví dụ như: số đối của số nguyên +1 là -1
3) giá bán trị hoàn hảo nhất của một trong những nguyên a chính là khoảng cách từ điểm a cho đến điểm 0 ngơi nghỉ trên trục số.
Ví dụ: |-20| = 20; |13| =13
4) Quy tắc cộng của hai số nguyên gồm cùng dấu: cùng tổng nhì số nguyên dương đó là cộng tổng nhì số thoải mái và tự nhiên có giá trị khác 0.
Ví dụ: (+4) + (+2) = 4 + 2 = 6
Để cộng tổng hai số nguyên âm, ta làm phép tính cùng hai giá bán trị tuyệt vời và hoàn hảo nhất của bọn chúng rồi để dấu “-” ở ngay trước công dụng tìm được.
Ví dụ: (-17) + (-55) = – (17 + 55) = -72
II. HÌNH HỌC (ÔN THI HỌC KÌ 1 LỚP 6 MÔN TOÁN)
1) Điểm – Đường thẳng| Cách viết thông thường | Hình vẽ | Kí hiệu |
| Điểm M | M | |
| Đường thẳng a | A | |
| Điểm M thuộc a | M ∈ d | |
| Điểm N ko thuộc a | N ∈ d |
Khi cha điểm nhưng cùng nằm trong (nằm trên) một con đường thẳng thì ta nói rằng bọn chúng thẳng hàng.
Khi tía điểm mà không thuộc thuộc (nằm trên) bất kỳ đường trực tiếp nào, ta nói rằng bọn chúng không trực tiếp hàng. Cho ví dụ, với ba điểm M,N,P vị trí một đường thẳng thì ta được:
– Điểm N, điểm p nằm sống trên cùng phía với điểm M.
– Điểm M, điểm phường nằm ở và một phía đối với điểm N.
Trong tía điểm thẳng sản phẩm này, tất cả duy độc nhất vô nhị một và có một điểm nằm ở vị trí giữa nhì điểm còn lại.
3) Đường thẳng trải qua hai điểmCó độc nhất vô nhị một cùng chỉ tất cả một con đường thẳng có thể đi qua nhị điểm phân biệt.
Hai mặt đường thẳng cơ mà không trùng nhau thì còn được gọi là hai đường thẳng phân biệt.
Hai mặt đường thẳng rõ ràng hoặc là chỉ có một điểm tầm thường (hai con đường thẳng giao nhau/ giảm nhau) hoặc không tồn tại một điểm tầm thường nào (hai mặt đường thẳng tuy vậy song).
4) TiaMột hình gồm có điểm O và 1 phần đường thẳng bị phân tách ra bởi vì một điểm O kia thì được hotline là tia nơi bắt đầu O (hay còn được gọi là một nửa đường thẳng gốc O).
Hai tia mà có chung nơi bắt đầu tia Ox với tia Oy và chế tạo thành được một đường thẳng xy, thì bó được call là nhì tia đối nhau. Mỗi điểm nằm trê tuyến phố thẳng các là gốc chung của nhì tia đối nhau.
Hai tia nhưng mà không trùng nhau thì còn gọi là hai tia phân biệt.
5) Đoạn thẳngĐoạn trực tiếp AB là một trong hình gồm có điểm A và điểm B và toàn bộ những điểm nằm ở giữa điểm A cùng điểm B. Điểm A với điểm B là nhị đầu (hoặc nhị mút) của đoạn thẳng AB.
6) Độ nhiều năm đoạn thẳngMỗi đoạn thẳng thì bao gồm một độ dài riêng. Độ nhiều năm của đoạn thẳng là 1 trong giá trị dương.
Hai đoạn trực tiếp AB và đoạn trực tiếp CD tất cả số đo bởi nhau, hay nói cách khác là bao gồm cùng một độ dài, được ký hiệu như sau: AB = CD. Đoạn thẳng EG tất cả độ dài lớn hơn (dài hơn) đối với đoạn trực tiếp CD thì sẽ được ký hiệu là EG > CD.
Đoạn thẳng IK bao gồm số đo ngắn thêm (nhỏ hơn) so với đoạn trực tiếp AB thì được ký kết hiệu là: IK
7) bao giờ thì AM + MB = AB?Nếu điểm M nằm ở phần giữa hai điểm A cùng điểm B trên thuộc một đường thẳng thì ta gồm phép tính: AM + MB = AB
Ngược lại, giả dụ như ta có công thức AM + MB = AB thì chắc chắn là điểm M nằm tại phần giữa nhì điểm A và điểm B.
8) Vẽ đoạn thẳng cho thấy thêm độ dàiỞ bên trên tia Ox thì lúc nào cũng rất có thể vẽ được độc nhất vô nhị một và duy nhất điểm M sao cho: OM = a (đơn vị độ dài)
Ở bên trên tia Ox, nếu như tất cả OM = a, ON = b cùng a
9) Trung điểm của đoạn thẳngTrung điểm M của một quãng thẳng AB là vấn đề nằm giữa hai điểm A với điểm B và bí quyết đều nhì điểm A với điểm B (ký hiệu là: MA = MB)
B. BÀI TẬP – ĐỀ ÔN THI TOÁN LỚP 6 HỌC KỲ 1
I. SỐ HỌC (ĐỀ ÔN THI TOÁN LỚP 6 HỌC KÌ 1)
Câu 1: Viết đa số tập phù hợp dưới đây bằng cách liệt kê ra các phần tử.
a) A={x ∈ N/ 42
b) B={x ∈ N*/ x
c) C= x ∈ N/ 23 ≤ x ≤ 26
Hướng dẫn: a. A = 43; 44; 45
Câu 2: Viết tập hòa hợp A các số từ nhiên bé dại hơn 5 cùng tập phù hợp B các số từ bỏ nhiên nhỏ tuổi hơn 6, rồi sử dụng kí hiệu ⊂ nhằm thể hiện mối quan hệ giữa nhị tập đúng theo trên.
Hướng dẫn: Liệt kê các thành phần của tập vừa lòng A cùng B.
Câu 3: Hãy tính số bộ phận của tập hòa hợp sau:
a) E= 19;21;23;…;99
b) F= 10;11;12;…;89
Hướng dẫn: vận dụng công thức (b – a) + 1
Câu 4: Tính nhanh
a) 27.36 + 27.64
b) 135 + 360 + 60 + 40
c) trăng tròn + 21 + 22 +…. + 29 + 30
Hướng dẫn: áp dụng các tính chất giao hoán, phối kết hợp phép nhân cùng phép cộng
Câu 5: tiến hành các phép tính
a) 3^6 : 3^2 + 2^3.2^2
b) 3.5^2 – 16 : 2^2
c) 80 – < 130 – (12 – 4)^2>
d) 5.7^2 – 24:2^3
e) (-5) + (+2) + +3 + (-4) + -1
f) (-17) + 5 + 8 + 17 + (-3)
Hướng dẫn: a) = 3^(6 – 2) + 2^(2 + 3)= 3^4 + 2^5 = 113
b) 71; c) 14 ; d) 242
Câu 6: tra cứu x, biết rằng:
a) 4 – (3x – 4) – 2 = 18
b) 256 – (x +71) = 92
c) (x – 45) – 320 = 0
Hướng dẫn:
a) x = 3
b) x = 93
c) x = 365
Câu 7: Xét coi tổng của những phép tính tiếp sau đây có phân tách hết đến 7 không?
a) 63 + 49 + 210
b) 42 + 60 + 280
c) 7560 + 18 + 3
Hướng dẫn: xét từng số hạng sinh hoạt trong phép tổng tất cả chia hết đến số 7 không?
Câu 8: cho những số 1345; 8520; 348; 2567. Trong những số đó:
a) Số nào phân tách được hết cho 2 nhưng không phân tách được hết cho 5?
b) Số nào phân tách được hết mang đến 5 mà không phân chia được hết đến 2?
c) Số nào chia được hết cho cả hai số 2 và số 5?
Hướng dẫn: Áp dụng những dấu hiệu của số phân chia hết mang đến số 2 với số 5?
Câu 9:Cho các số: 4316; 7164; 657; 1248.
a) Viết tập đúng theo A chia hết được cho 3
b) Viết tập đúng theo B phân tách hết được cho 9
c) cần sử dụng kí hiệu ⊂ thể hiện quan hệ giữa A và B.
Hướng dẫn: áp dụng những dấu hiệu của số phân chia được hết cho số 3 với số 9.
Câu 10: nỗ lực a và b vì chưng những chữ số say mê hợp, biết rằng:
a) Số 4a2b chia hết cho 2;5 và 9
b) Số 2a36b chia hết 5;9 mà lại không phân chia hết mang lại 2.
c) Số a63b chia hết mang lại 2;3;5 cùng 9.
Hướng dẫn: áp dụng những tín hiệu của số phân chia được hết mang lại số 2,3,5 và 9.
Xem thêm: Hình ảnh chiếc máy tính đầu tiên trên thế giới, chiếc máy tính điện tử đầu tiên của thế giới
Câu 11: tìm ra số tự nhiên x, sao cho:
a) x ∈ B(9) cùng 27 ≤ x ≤ 71
b) x phân chia hết đến 12 và 0
c) 18 x
Hướng dẫn: a. Ta có: x = B(9) = 0;9;18;27;36;45;54;63;72;81;…. Mà lại 27 ≤ x ≤ 71 nên x = 27;36;45;54;63
Câu 12: search ƯCLN:
a) đôi mươi và 30
b) 13 với 15
c) 9; 36 và 54
Hướng dẫn: vận dụng những quy tắc để tìm ra được ƯCLN.
Câu 13: tra cứu BCNN:
a) 30 với 280
b) 17 và 15
c) 12; 48 với 72
Hướng dẫn: vận dụng những quy tắc nhằm tìm ra được BCNN.
Câu 14:
a) tìm số tự nhiên và thoải mái a to nhất, hiểu rằng rằng: 520a và 480a
b) Tìm hồ hết ước chung to hơn số 30 của số 144 cùng 192
c) tìm kiếm x, biết rằng: 122 chia được hết cho x; 420 phân tách được hết đến x với 10
Hướng dẫn:
a) ƯCLN(520,480) = ?
b) x = ƯC(144,192) >30
c) 10
Câu 15:
a) tìm kiếm số tự nhiên a có giá trị nhỏ nhất khác 0, hiểu rằng rằng a30 và a18
b) Tìm phần lớn bội chung bé dại hơn 500 của số 18 và số 45
c) search x, hiểu được x4; x21; x28 và 165
Hướng dẫn:
a) a = BC(30,18)
b) BC(18,45)
c) 165
Câu 16:
a) thu xếp những số sau theo một sản phẩm tự tăng đột biến là: 5; -105; -5; 1; 0; -3; 15
b) bố trí những số sau theo một vật dụng tự bớt dần là: -125; 21; 0;-175; 4; -2001; 2001
Câu 17: Tính giá bán trị của rất nhiều biểu thức sau:
a) |-25| – |-5|
b) |+136| : |-17|
c) |-125| : |-5|
d) |375| + |-25|
Hướng dẫn: a.20; b.8; c.25; d.400
Câu 18: tìm kiếm x ∈ Z, biết:
a) -9
b) -3
c) -5 ≤ x ≤ 5
d) 0
Hướng dẫn: Liệt kê những thành phần của tập đúng theo đó.
Câu 19: tìm thấy số nguyên x, biết rằng:
a) |x| =2; |x| =6; |x| = 0
b) |x| =2 với x>0
|x| =5 với x
Hướng dẫn: a. X = -2 cùng x = 2
Câu 20: Tính
a) (-15) + (-585)
b) 42 + (-38)
c) (-75) + (+35)
d) (-85) + 0
e) |-67| + |-17|
f) 315 + (-435)
g) (-50) + (-35)
h) (-16) + (-14)
i) (-250) + (+250)
Hướng dẫn: a.-600; b.4; c.-40; d.-85; e.84; f.-120; g.-85; h.-30; i.0
Câu 21: Tính tổng của các giá trị của x ∈ Z, thỏa mãn được:
a) -3
b) -8
Hướng dẫn: a. X = -2;-1;0;1;2;3;4;5;6
Tổng = (-2 + 2) + (-1 + 1) + 0 +3 + 4 +5 +6 = 18
Câu 22: Tính
a) 1999 + (-2000) + 2001 + (-2002)
b) 49 – (-54) – 23
c) (-25).68 + (-34).(-250)
Hướng dẫn: a.-2; b.80; c.6800
Câu 23: Tính nhanh:
a) 515 + <72 + (-515) + (-32)>
b) Tổng tất cả các số nguyên có giá trị xuất xắc đối bé dại hơn hoặc bởi 7.
Hướng dẫn: a. 40; b. 0
Câu 24: Tính nhanh hầu hết biểu thức sau:
a) (2736 – 75) – 2736
b) (-2002) – (57 – 2002)
c) (9765 – 115) – 9765
d) (-3076) – (75 – 3075)
Hướng dẫn: a.-75; b.-57; c.-115; d.-75
Câu 25: Tìm hầu hết số nguyên x, biết:
a) x + |-2| = 0
b) 2x – +4 = 6
c) x + 5 = đôi mươi – (12 – 7)
d) 15 – (3 + 2x) = 22
e) -11 – (19 – x) = 50
f) (7 + x) – (21 -13) = 32
Hướng dẫn: a. X = -2; b. X = 5; c. X = 10; d. X = 4; e. X = 80; f. X = 33
Câu 26: Tính nhanh đầy đủ tổng sau:
a) (-25) + 8 +12 +25
b) 40 +15 +(-10) + (-15)
c) -13 + (-750) + (-17) + 750
d) (-7) + (-20) + 35 + (-8)
Hướng dẫn: a.20; b.30; c.-30; d.0
Câu 27: vứt đi dấu ngoặc rồi tính:
a) (35 – 17) + (17 + đôi mươi – 35)
b) (55 + 45 + 15) – (15 – 55 + 45)
Hướng dẫn: a.20; b.110
Câu 28: một tổ y tế gồm tất cả 24 chưng sĩ và 108 y tá rất có thể được chia các nhất thành mấy tổ để số bác sĩ cũng giống như là số y tá được chia phần lớn vào trong những tổ đó.
Hướng dẫn: ƯCLN(24, 108) ?
Câu 29: Trong một trong những buổi liên hoan, ban tổ chức đã download 96 mẫu bánh, 36 mẫu kẹo cùng chia những ra từng đĩa, mỗi đĩa gồm tất cả cả kẹo cùng bánh. Ta hoàn toàn có thể chia được thành nhiều nhất là bao nhiêu đĩa, mỗi đĩa chứa từng nào cái kẹo và từng nào cái bánh?
Hướng dẫn: ƯCLN(96, 36) ?
Câu 30: Số lượng học sinh khối 6 của trường trong khoảng tầm trường đoản cú 200 cho tới 400. Lúc ta xếp hàng 15, sản phẩm 18 thì phần đa thừa 5 học tập sinh. Tính ra số học sinh đó?
Hướng dẫn: BCNN(15, 18) ?
Câu 31: An, Ngọc, Bảo đang trực nhật chung với nhau trong ngày hôm nay. Biết rằng chúng ta An cách 4 ngày trực nhật một lần, các bạn Bảo cách 8 ngày trực một lần. Chúng ta Ngọc giải pháp 6 ngày trực nhật một lần. Hỏi sau mấy ngày thì An, Ngọc, Bảo trực nhật thông thường lần tiếp theo?
Hướng dẫn: BCNN(4, 6, 8) ?
II. HÌNH HỌC (ĐỀ ÔN THI TOÁN LỚP 6 HỌC KÌ 1)
Câu 1: cho những điểm A; B; C; D; E theo vật dụng tự ở trên thuộc một mặt đường thẳng.
a) Điểm C nằm tại giữa 2 điểm nào?
b) Điểm C không nằm tại vị trí giữa 2 điểm nào?
c) có bao nhiêu đoạn thẳng ở trên hình vẽ?
Câu 2: mang đến hai tia OA cùng tia OB giao nhau trên điểm O.
Trên tia OA ta mang điểm C làm sao cho điểm A nằm trong lòng điểm O cùng điểm C. Bên trên tia OB ta lấy điểm D làm sao để cho điểm D nằm trong lòng điểm O cùng điểm B. Vẽ nhị đoạn thẳng AB với đoạn thẳng CD. Call E là giao điểm của nhị đoạn thẳng AB và đoạn trực tiếp CD. Vẽ đoạn trực tiếp OE.
Câu 3: bên trên tia Ox lấy hai điểm A với điểm B sao cho ta có: OA = 2(cm); OB = 5(cm). Bên trên tia đối của tia BO ta rước điểm C sao cho: BC = 3(cm). Tính giá trị độ nhiều năm AC.
Hướng dẫn: AC = 6
Câu 4: gọi I là một trong những điểm thuộc đoạn trực tiếp KN. Biết rằng IK=2(cm); IN=3(cm). Tính quý giá độ lâu năm đoạn trực tiếp KN.
Hướng dẫn: KN = 5
Câu 5: call N là một trong điểm thuộc đoạn trực tiếp CD. Biết rằng CD=6(cm); CN=3(cm). So sánh độ nhiều năm của nhị đoạn thẳng công nhân và đoạn trực tiếp ND.
Hướng dẫn: công nhân
Câu 6: bên trên tia Ox, vẽ đem hai đoạn trực tiếp OP = 2(cm) với OQ = 4(cm). Tính giá trị độ nhiều năm đoạn PQ. So sánh độ nhiều năm của đoạn OP cùng đoạn PQ.
Hướng dẫn: PQ = 2(cm); OP =OQ
Câu 7: Đoạn thẳng AC bao gồm độ nhiều năm là 5 cm. Điểm B nằm trong lòng điểm A với điểm C thế nào cho BC=2 (cm).
a) Tính AB.
b) trên tia đối của tia cha lấy Điểm D sao cho: BD=5(cm). Tính AD với CD.
Hướng dẫn: a. AB = 3(cm); b. AD = 8(cm); CD = 3(cm)
Câu 8: bên trên tia Ax rước hai điểm B cùng điểm C sao cho AB=4(cm); AC=2(cm).
a) Điểm C có nằm giữa điểm A với điểm B hay không? lý giải lý vì vì sao?
b) Điểm C tất cả là trung điểm của đoạn trực tiếp AB hay không? giải thích lý vày vì sao?
Hướng dẫn:
a) Điểm C có nằm giữa điểm A với điểm B vì tía điểm A,B,C thuộc nằm trên một mặt đường thẳng cùng ta tất cả AB > AC.
b) Điểm C tất cả là trung điểm của đoạn thẳng AB do điểm C nằm giữa điểm A với điểm B và ta có AC = BC.
→ Tham khảo cụ thể Đề cưng cửng ôn thi học kì 1 môn toán lớp 6 ngay lập tức tại trên đây (↓):
Đề cương cứng ôn thi Ngữ văn lớp 6 học kì 1
Đề cương ôn thi tiếng Anh lớp 6 học kì 1
Vậy là chúng ta đã cùng nhau kết thúc bài Đề cưng cửng ôn thi toán 6 học kì 1 rồi các em học viên khối 6 thân yêu. Những em đã nắm rõ được những kiến thức và kỹ năng cốt lõi làm việc trong bài xích chưa nhỉ? các em hãy đừng quên truy cập hoctot.hocmai.vn để tham khảo thêm thật nhiều bài học bổ ích, những loại câu đặc biệt quan trọng nữa nhé!
Lớp 1Đề thi lớp 1
Lớp 2Lớp 2 - kết nối tri thức
Lớp 2 - Chân trời sáng sủa tạo
Lớp 2 - Cánh diều
Tài liệu tham khảo
Lớp 3Lớp 3 - kết nối tri thức
Lớp 3 - Chân trời sáng sủa tạo
Lớp 3 - Cánh diều
Tài liệu tham khảo
Lớp 4Sách giáo khoa
Sách/Vở bài xích tập
Đề thi
Lớp 5Sách giáo khoa
Sách/Vở bài bác tập
Đề thi
Lớp 6Lớp 6 - liên kết tri thức
Lớp 6 - Chân trời sáng tạo
Lớp 6 - Cánh diều
Sách/Vở bài tập
Đề thi
Chuyên đề và Trắc nghiệm
Lớp 7Lớp 7 - kết nối tri thức
Lớp 7 - Chân trời sáng tạo
Lớp 7 - Cánh diều
Sách/Vở bài bác tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 8Sách giáo khoa
Sách/Vở bài bác tập
Đề thi
Chuyên đề & Trắc nghiệm
Lớp 9Sách giáo khoa
Sách/Vở bài xích tập
Đề thi
Chuyên đề và Trắc nghiệm
Lớp 10Lớp 10 - liên kết tri thức
Lớp 10 - Chân trời sáng sủa tạo
Lớp 10 - Cánh diều
Sách/Vở bài tập
Đề thi
Chuyên đề và Trắc nghiệm
Lớp 11Sách giáo khoa
Sách/Vở bài bác tập
Đề thi
Chuyên đề và Trắc nghiệm
Lớp 12Sách giáo khoa
Sách/Vở bài tập
Đề thi
Chuyên đề và Trắc nghiệm
ITNgữ pháp giờ đồng hồ Anh
Lập trình Java
Phát triển web
Lập trình C, C++, Python
Cơ sở dữ liệu

Bộ đề thi Toán lớp 6 sách mới
Bộ đề thi Toán lớp 6 - liên kết tri thức
Bộ đề thi Toán lớp 6 - Cánh diều
Bộ đề thi Toán lớp 6 - Chân trời sáng tạo
Top 30 Đề thi học tập kì 1 Toán lớp 6 gồm đáp án (sách mới) | kết nối tri thức, Cánh diều, Chân trời sáng chế
Top 30 Đề thi học kì 1 Toán lớp 6 tất cả đáp án sách mới liên kết tri thức, Cánh diều, Chân trời sáng chế được biên soạn bám sát đít chương trình Toán 6 bắt đầu năm 2022 - 2023. Hy vọng bộ đề thi này sẽ giúp đỡ bạn ôn tập & đạt điểm cao trong các bài thi Toán lớp 6.
Top 30 Đề thi học tập kì 1 Toán lớp 6 gồm đáp án (sách mới) | kết nối tri thức, Cánh diều, Chân trời sáng tạo
Để tải trọn bộ Đề thi Toán 6 phiên bản word có giải thuật chi tiết, đẹp mắt, quý Thầy/Cô vui vẻ truy cập tailieugiaovien.com.vn
- bộ sách Kết nối tri thức với cuộc sống
Quảng cáo
- cuốn sách Cánh diều
- cuốn sách Chân trời sáng tạo
Quảng cáo
Phòng giáo dục và Đào sản xuất ...
Đề thi học tập kì 1 Toán 6
Năm học tập 2022 - 2023
Thời gian làm cho bài: 90 phút
(không kể thời gian phát đề)
(Đề 1)
(Kết nối tri thức)
I. Trắc nghiệm (2 điểm)
Câu 1: Biết 143 - x = 57, cực hiếm của x là
A) 86
B) 200
C) 144
D) 100
Câu 2: Chiếc đồng hồ đeo tay gỗ sau đây có làm nên gì:

A) Tam giác
B) Hình vuông
C) Hình chữ nhật
D) Hình lục giác đều
Câu 3: Cho hình vuông vắn ABCD. Xác minh sai là:
A) hình vuông vắn ABCD có bốn cạnh bởi nhau: AB = BC = CD = AD.
B) hình vuông vắn ABCD gồm bốn góc ở đỉnh A; B; C; D bằng nhau.
C) hình vuông vắn ABCD có hai đường chéo cánh bằng nhau: AC = BD.
D) hình vuông ABCD tất cả hai cặp cạnh đối tuy vậy song AB và BC; CD và AD.
Câu 4: Tập hợp những ước chung của 12 và đôi mươi là:
A) 1; 2; 4; 5
B) 2; 4; 5
C) 1; 2; 4
D) 1; 4; 5; 15
Câu 5: Số đối của số đôi mươi là:
A) 1
B) 0
C) -1
D) -20
Câu 6: Tam giác với hình vuông bên dưới có chu vi bằng nhau. Độ dài cạnh của hình vuông dưới là:
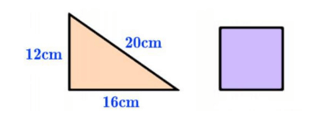
A) 8cm
B) 12cm
C) 16cm
D) 24cm
Câu 7: tất cả bao nhiêu số nguyên x thoản mãn -4 Quảng cáo
II. Tự luận
Bài 1 (2 điểm): thực hiện phép tính
a) 22.85 + 15.22 - 20200
b) 50 + <65 - (9 - 4)2>
c) (39 - 19) : (-2) + (34 - 22).5
d) 123.456 + 456.321 – 256.444
Bài 2 (1,5 điểm): search x
a) 3x – 2 = 19
b) <43 - (56 - x)>.12 = 384
c) 3x.2 + 15 = 33
Bài 3 (2 điểm): Cô Hoa ước ao lát nền cho 1 căn phòng ở trong phòng mình gồm hình chữ nhật với chiều nhiều năm là 8m với chiều rộng là 5m. Các loại gạch lát nền được thực hiện là gạch men vuông bao gồm cạnh 40cm. Hỏi cô Hoa phải áp dụng bao nhiêu viên gạch ốp (coi mạch xi măng không xứng đáng kể).
Bài 4 (2 điểm): các bạn Hà tất cả 42 viên bi màu đỏ và 30 viên bi màu sắc vàng. Hà rất có thể chia những nhất vào từng nào túi làm thế nào để cho số bi đỏ và bi tiến thưởng được chia đều vào các túi? khi ấy mỗi túi bao gồm bao nhiêu viên bi đỏ và vàng.
Bài 5 (0,5 điểm): tra cứu cặp số thoải mái và tự nhiên x, y biết: (x + 5)(y - 3) = 15.
Đáp án
I. Trắc nghiệm (2 điểm)
Câu 1: Biết 143 - x = 57, cực hiếm của x là
A) 86
B) 200
C) 144
D) 100
Giải thích:
x = 143 – 57
x = 86
Câu 2: Chiếc đồng hồ gỗ sau đây có ngoài mặt gì:

A) Tam giác
B) Hình vuông
C) Hình chữ nhật
D) Hình lục giác đều
Giải thích: Ta đếm được chiếc đồng hồ là hình tất cả 6 cạnh và tiến hành đo bởi thước kẻ thấy 6 cạnh đó đều bằng nhau nên là lục giác đều
Câu 3: Cho hình vuông ABCD. Khẳng định sai là:
A) hình vuông ABCD bao gồm bốn cạnh bởi nhau: AB = BC = CD = AD.
B) hình vuông vắn ABCD bao gồm bốn góc ngơi nghỉ đỉnh A; B; C; D bằng nhau.
C) hình vuông vắn ABCD bao gồm hai đường chéo cánh bằng nhau: AC = BD.
D) hình vuông ABCD tất cả hai cặp cạnh đối song song AB và BC; CD và AD.
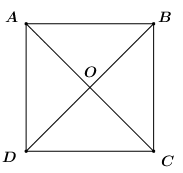
Giải thích:
A) đúng do bốn cạnh AB; BC: CD; AD bởi nhau
B) đúng bởi vì bốn góc ngơi nghỉ đỉnh A; B; C; D bằng nhau.
C) đúng vì có hai đường chéo bằng nhau: AC = BD
D) sai do AB với BC; CD và AD chưa phải các cạnh đối vì thế nó không tuy nhiên song.
Câu 4: Tập hợp các ước chung của 12 và 20 là:
A) 1; 2; 4; 5
B) 2; 4; 5
C) 1; 2; 4
D) 1; 4; 5; 15
Giải thích:
12 = 2.2.3 = 22.3
20 = 2.2.5 = 22.5
ƯCLN (12; 20) = 22 = 4
ƯC (12; 20) = 1; 2; 4
Câu 5: Số đối của số trăng tròn là:
A) 1
B) 0
C) -1
D) -20
Giải thích: Số đối của số trăng tròn là -20 vì trăng tròn + (-20) = 0
Câu 6: Tam giác và hình vuông bên dưới có chu vi bởi nhau. Độ nhiều năm cạnh của hình vuông dưới là:
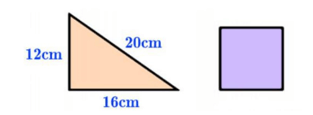
A) 8cm
B) 12cm
C) 16cm
D) 24cm
Giải thích: Chu vi tam giác là: 12 + 16 + đôi mươi = 48 (cm)
Do chu vi tam giác bằng chu vi hình vuông vắn nên chu vi hình vuông vắn là 48cm
Độ dài cạnh hình vuông là: 48:4 = 12 (cm)
Câu 7: có bao nhiêu số nguyên x thoản mãn -4 B) 6
C) 5
D) 8
Giải thích: Tập số nguyên x thỏa mãn nhu cầu -4 B) x = 4; y = 0
C) x = 0; y = 4
D) x = 8; y = 5.
Giải thích: Để
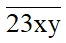
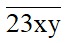
Ta có: 2 + 3 + x + 0 = 5 + x
Mà x, y ∈ ℕ*; 0 ≤ x, y ≤ 9 cần ta gồm x = 4 (vì 5 + 4 = 9 phân tách hết mang đến 3 và chia hết cho 9).
Vậy x = 4; y = 0.
II. Từ bỏ luận
Bài 1 (2 điểm):
a) 22.85 + 15.22 - 20200
= 4.85 + 15.4 – 1
= 4.(85 + 15) – 1
= 4.100 – 1
= 400 – 1
= 399
b) 50 + <65 - (9 - 4)2>
= 50 +
= 50 + <65 – 25>
= 50 + 40
= 90
c) (39 - 19) : (-2) + (34 - 22).5
= đôi mươi : (-2) + 12.5
= -10 + 60
= 50
d) 123.456 + 456.321 – 256.444
= 456.(123 + 321) – 256.444
= 456.444 – 256.444
= 444.(456 – 256)
= 444
Bài 2 (1,5 điểm):
a) 3x – 2 = 19
3x = 19 + 2
3x = 21
x = 21:3
x = 7
b) <43 - (56 - x)>.12 = 384
43 – (56 – x) = 384:12
43 – (56 – x) = 32
56 – x = 43 – 32
56 – x = 11
x = 56 – 11
x = 45
c) 3x.2 + 15 = 33
3x.2 = 33 - 15
3x.2 = 18
3x = 18 : 2
3x = 9
3x = 33
x = 2.
Bài 3 (2 điểm):
Đổi 8m = 800cm
5m = 500cm
Diện tích căn phòng là: 500.800 = 400 000 (cm2)
Diện tích một viên gạch là: 40.40 = 1600 (cm2)
Số viên gạch cô Hoa cần dùng làm lát sàn nhà là:
400000 : 1600 = 250 (viên)
Bài 4 (2 điểm):
Gọi số túi bi chia được không ít nhất là x ( x ∈ ℕ*)
Vì số bi đỏ với vàng từng túi là gần như nhau cần 42 ⋮ x và 30 ⋮ x. Vì thế x là ước tầm thường của 42 và 30.
Mặt khác x lớn nhất (chia vào các túi nhất) phải x là mong chung lớn số 1 của 42 và 30.
Ta có:
42 = 2.3.7
30 = 2.3.5
ƯCLN (42; 30) = 2.3 = 6
Vậy x = 6
Khi đó:
Số bi màu rubi mỗi túi là
30: 6 = 5 (viên)
Số bi red color mỗi túi là
42: 6 = 7 (viên)
Bài 5 (0,5 điểm): tra cứu cặp số thoải mái và tự nhiên x, y biết: (x + 5)(y - 3) = 15
(x + 5)(y - 3) = 15
(x + 5)(y – 3) = 1.15 = 15.1 = 3.5 = 5.3
Trường phù hợp 1: với x + 5 = 1 (vô lí vị x, y ∈ ℕ)
Trường hợp 2: cùng với x + 5 = 15 thì x = 10
Khi đó: y – 3 = 1 thì y = 4
Trường phù hợp 3: với x + 5 = 3 (vô lí bởi vì x, y ∈ ℕ)
Trường hòa hợp 4: cùng với x + 5 = 5 thì x = 0
Khi đó: y – 3 = 3 thì y = 6.

Phòng giáo dục và đào tạo và Đào sản xuất ...
Đề thi học kì 1 Toán 6
Năm học 2022 - 2023
Thời gian làm cho bài: 90 phút
(không kể thời hạn phát đề)
(Đề 1)
(Cánh diều)
I. Phần trắc nghiệm (3 điểm)
Câu 1: Tập hòa hợp B = B = 0; 1; 2; ...; 100 bao gồm số thành phần là:
A) 99
B) 100
C) 101
D) 102
Câu 2: Tìm xác minh đúng trong các khẳng định sau:
A) một trong những chia hết mang lại 9 thì luôn chia hết đến 3.
B) nếu hai số phân tách hết cho 3 thì tổng của hai số đó chia hết mang đến 9.
C) phần đa số chẵn thì luôn chia hết mang lại 5.
D) Số chia hết mang đến 2 là số có chữ số tận cùng bằng 0; 2; 3; 4; 6; 8.
Câu 3: Hình không tồn tại tâm đối xứng là:
A) Hình tam giác
B) Hình chữ nhật
C) Hình vuông
D) Hình lục giác đều.
Câu 4: Cách viết nào dưới đây được điện thoại tư vấn là so sánh số 80 ra vượt số nguyên tố.
A) 80 = 42.5
B) 80 = 5.16
C) 80 = 24.5
D) 80 = 2.40
Câu 5: Khẳng định nào dưới đây đúng
A) Hình thoi bao gồm hai đường chéo bằng nhau.
B) hình vuông vắn có tứ cạnh bằng nhau.
C) Hình chữ nhật bao gồm hai đường chéo vuông góc với nhau.
D) Hình thang gồm hai đường chéo cánh bằng nhau.
Câu 6: vật dụng tự triển khai phép tính trong biểu thức: A = 126 : (42 + 2) là:
A) Phép phân chia – phép cùng – lũy thừa.
B) Phép cùng – lũy quá – phép chia.
C) Lũy quá – phép cùng – phép chia.
D) Lũy quá – phép chia – phép cộng.
II. Phần tự luận
Bài 1 (2 điểm): triển khai phép tính:
a) 667 – 195.93:465 + 372
b) 350.12.173 + 12.27
c) 321 - 21.<(2.33 + 44 : 32) - 52>
d) 71.64 + 32.(-7) – 13.32
Bài 2 (2 điểm): search x
a) x + 72 = 0
b) 3x + 10 = 42
c) (3x - 1)3 = 125
d) (38 - x)(x + 25) = 0
Bài 3 (1,5 điểm): một nhóm y tế gồm gồm 220 con gái và 280 nam dự định tạo thành các nhóm thế nào cho số nữ giới và số nam sinh sống mỗi nhóm đa số nhau, biết số đội chia được không ít hơn 1 nhóm và không to hơn 5 nhóm. Hỏi gồm thể phân thành mấy nhóm? khi ấy mỗi nhóm bao gồm bao nhiêu nam từng nào nữ.
Bài 4 (1 điểm): Tính chu vi và ăn mặc tích hình chữ nhật tất cả chiều lâu năm là 27cm cùng chiều rộng là 15cm.
Bài 5 (0,5 điểm): mang lại A = 1 + 3 + 32 + 33 + ... + 3100. Chứng tỏ A phân chia hết mang đến 13.
Đáp án
I. Phần trắc nghiệm (3 điểm)
Câu 1: Tập phù hợp B = bao gồm số thành phần là:
A) 99
B) 100
C) 101
D) 102
Giải thích:
Số bộ phận của tập hợp ta sẽ tính theo công thức tính số số hạng.
Số bộ phận của tập vừa lòng B là: (100 – 0):1 + 1 = 101 (số)
Câu 2: Tìm xác minh đúng vào các khẳng định sau:
A) một vài chia hết cho 9 thì luôn chia hết mang lại 3.
B) trường hợp hai số phân chia hết đến 3 thì tổng của hai số đó phân chia hết đến 9.
C) phần nhiều số chẵn thì luôn luôn chia hết mang đến 5.
D) Số chia hết mang lại 2 là số có chữ số tận cùng bởi 0; 2; 3; 4; 6; 8.
Giải thích:
A) đúng do số chia hết đến 9 gồm dạng 9k mà lại 9k = 3.3.k = 3.(3k) phân chia hết mang lại 3
B) sai vì chưng 6 cùng 9 phân tách hết cho 3 mà lại tổng của 6 với ư9 là 15 lại không phân chia hết mang đến 9.
C) sai vị 42 là số chẵn tuy nhiên không phân chia hết cho 5.
D) Sai vì chưng số gồm tận cùng là 3 không phân tách hết đến 2 lấy một ví dụ 33 không phân chia hết mang đến 2.
Câu 3: Hình không tồn tại tâm đối xứng là:
A) Hình tam giác
B) Hình chữ nhật
C) Hình vuông
D) Hình lục giác đều.
Giải thích:
Tâm đối xứng của hình chữ nhật, hình vuông, hình lục giác số đông được màn trình diễn dưới hình sau









